TP #1 de C++ : implémentation de classes simples

Exercice n°1 : la classe Individu

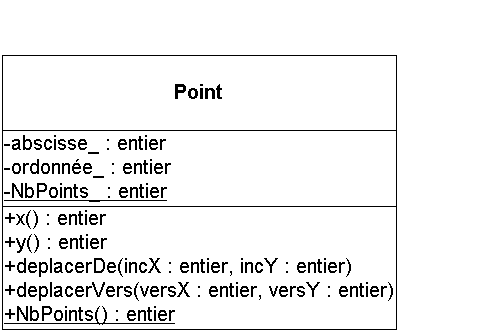
Le but de cet exercice est d'implémenter la classe Individu dont le schéma est donné ci-dessous :

Vous tiendrez compte des éléments suivants :

• Les caractères accentués sont interdits en C++
• On ne créera qu'un seul constructeur pour la classe Individu. Celui permettra d'initialiser tous les attributs. Seul le paramètre permettant d'initialiser la profession pourra avoir une valeur par défaut.
• La méthode obtenirDateDeNaissance crée une chaîne sous la forme "JJ/MM/AA" à partir des informations placées dans les attributs idoines.
• Conceptuellement l'état civil d'un individu ainsi que sa date de naissance ne changent pas : on ne fournira donc pas d'accès en modification sur ces attributs.
• L'attribut de classe TaillePopulation est destiné à recenser à chaque instant le nombre exact d'individus, tenez en compte dans votre constructeur et votre destructeur.
• Les méthodes d'accès aux informations seront codées inline, le constructeur devra être quand à lui externalisé.

Une petite indication : la réalisation de cet exercice implique de manipuler des tableaux de caractères pour stocker des chaînes de caractères. La fonction strdup qui alloue un tableau de caractères avant de l'initialiser doit être proscrite car elle appelle malloc, lequel est bani du C++. Voici donc un extrait de code qui permet d'initialiser un pointeur de caractères à partir d'une chaîne :

char *nouvelle;
char ancienne[]="Chaine a recopier";

nouvelle=new char[strlen(ancienne)+1]; // Allocation du tableau
strcpy(nouvelle,ancienne);             // Recopie

Exercice n°2 la classe NombreComplexe 1^ère partie

Motivation

Un nombre complexe admet 2 représentations :

• La forme cartésienne a+ib où a s'appelle partie réelle et b partie imaginaire.
• La forme polaire : un couple (mode, argument)

La figure suivante illustre comment passer de la forme cartésienne à la forme polaire et réciproquement.

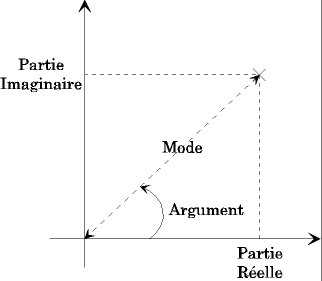
En fait, l'on a :

1. a=mode × cos(arg)
2. b=mode × sin(arg)

Et :

1. mode=sqrt(a²+b²)
2. arg=atan2(a,b) … pas tout à fait exact, mais ça simplifie !

Les deux formes étant duales, il n'y a pas de raison de choisir l'une plus que l'autre pour la représentation interne. En outre, l'utilisateur n'a pas à se soucier de cette différence de stockage. Aussi, nous fournirons 4 méthodes permettant de récupérer les coordonnées dans les 2 systèmes ainsi que 2 méthodes permettant de modifier un nombre complexe dans chacune de ses représentations.

La figure suivante illustre la classe NombreComplexe si l'on utilise une représentation interne cartésienne.

Reste à régler le problème du constructeur. Idéalement, il serait agréable de disposer de 2 constructeurs, l'un en mode cartésien et l'autre en mode polaire, tel que suggéré par le fragment de code suivant :

NombreComplexe::NombreComplexe(double a, double b);
NombreComplexe::NombreComplexe(double mode, double argument);

Hors ceci n'est pas possible car les signatures d'arguments sont identiques. La solution consiste donc à créer un constructeur par défaut initialisant le nombre complexe à une valeur facile à identifier dans les deux systèmes : l'origine. Les méthodes modifierCartésien et modifierPolaire permettront ensuite d'obtenir un nombre quelconque dans le système choisi.

Travail à réaliser

1. Implémenter la classe NombreRationnel en utilisant la représentation interne sous forme cartésienne. Toutes les méthodes seront codées inline.
2. Créez diverses instances :
   • Statiques
   • Automatiques
   • Dynamiques
   • Tableau Statique d'instances Statiques
   • Tableau Dynamique d'instances Statiques
   • Tableau Statique d'instances Dynamiques
   • Tableau Dynamique d'instances Dynamiques
3. Ajoutez une méthode nommée print et permettant d'afficher un NombreComplexe. Pour cette fois, vous utiliserez la fonction printf. Effectuez alors un certain nombre d'opérations sur vos complexes et imprimez le résultat.
4. Changez la représentation interne depuis le mode cartésien vers le mode polaire et recommencez les expériences ci-dessus. Vous pourrez ainsi vérifier le bien fondé de la séparation de l'interface par rapport à l'implémentation

Exercice 3 : la classe Point

A la suite de la classe NombreComplexe et des explications vues en cours, codez la classe Point telle qu'explicitée sur la figure ci-dessous :.